Veri-İstatistik
Veri-İstatistik
Merkezi Eğilim Ölçüleri
Gözlenen verilerin düzenlenerek, tablolarla, grafiklerle sunulması çoğu durumda yeterli olmaz. Genel durumu yansıtacak bir takım ölçülere gereksinim vardır. Bu ölçüler merkezi eğilim ölçüleri olup en çok kullanılanları;
Aritmetik Ortalama
Bir veri dizisindeki terimlerin toplamının terim adedine bölünmesiyle bulunur. x̅ ile gösterilir.

Örnek
7, 6, 7, 8, 10, 12, 6 veri grubundaki sayıların ortalaması kaçtır?
Çözüm
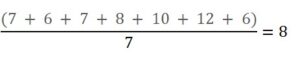
Ortanca (Medyan)
Terim sayısı tek sayı ise medyan tam ortadaki terimdir. Medyan terimlerden biridir. Terim sayısı çift sayı ise medyan ortadaki iki terimin aritmetik ortalamasıdır. Medyan terimlerden biri olmayabilir.
*Dizinin terim sayısı tek ise ortadaki terim ortancadır.
*Dizinin terim sayısı çift ise ortadaki iki terimin aritmetik ortalaması ortancadır.
Örnek
Örnek: Bir markette peynir fiyatları aşağıdaki gibidir: 6, 12, 15, 4, 8. Medyan fiyat nedir?
• 4
• 6
• 8 Dizin sıralandıktan sonra ortadaki değer medyandır.
• 12
• 15
Tepe Değer (Mod)
Bir veri grubundaki en çok (en sık) tekrarlanan değere Tepe değeri (Mod) denir. Tekrar sayıları frekans olarak adlandırılır. Bir veri grubunda birden fazla tekrar eden değer yoksa, bu veri grubunun tepe değeri yoktur.
Bir veri grubunda aynı sayıda tekrar eden birden fazla değer varsa, tepe değeri de birden fazla olabilir. Fakat, tüm değerler eşit sayıda tekrar ediyorsa tepe değeri yoktur. Ardışık olan tepe değerlerinin ortalaması alınır.
Örnek
3, 5, 5, 6, 7, 7, 7, 8, 10 veri grubunun tepe değerini bulalım.
En çok tekrar eden veri 7 olduğu için tepe değer 7’dir.
Merkezi Yayılım (Dağılım) Ölçüleri
Açıklık (Aralık – Ranj)
Sonlu bir veri grubunda en büyük terimden en küçük terimi çıkartarak bulunan değerdir.
R = En Büyük Değer – En Küçük Değer
Örnek
7, 3, 4, 9, 2, 7, 5 veri grubunun açıklığını (Ranjını) bulunuz.
Çözüm: R = 9 – 2 = 7 dir.
Örnek
26, 16, 16, 33, 55, 109 sayılarından en büyük olan 109 en küçük olan 16 dır.
Buna göre verilen sayıların açıklığı, 109 – 16 = 93 tür.
Çeyrekler Açıklığı
Bir veri grubundaki terimler küçükten büyüğe doğru sıralandığında ilk terime en küçük, son terime en büyük, bunların ortasındaki terime de ortanca denir.
Ortancadan küçük olan terimlerin ortancasına alt çeyrek (Q1) denir.
Ortancadan büyük olan terimlerin ortancasına üst çeyrek(Q3) denir.
Bir başka ifade ile veri kümesinin ilk % 50 lik kısmının ortancasına Q1 , sonraki % 50 lik kısmının ortancasına da Q3 denir.
Örnek
2, 3 , 6, 9, 5, 10, 4, 2, 9, 8, 5 verilerinin oluşturduğu grubun çeyrekler açıklığını bulalım.
Verileri küçükten büyüğe sıraya koyalım.
2, 2, 3, 4, 5, 5, 6, 8, 9, 9, 10
Ortanca terim, alt uçtan ve üst uçtan eşit uzaklıkta olan terimdir. Veya Q=1/2(n+1) inci terimdir. 6. terim yapar
2, 2, 3, 4, 5, 5, 6, 8, 9, 9, 10
ortanca terim( Medyan)
Alt çeyrek: 2, 2, 3, 4, 5 verilerinin ortadaki elemanı olan 3 tür.
Üst çeyrek: 6, 8, 9, 9, 10 verilerinin ortadaki elemanı olan 9 dur
Çeyrekler açıklığı: 9 – 3 = 6 bulunur.
Standart Sapma
Sonlu bir nicel veri dizisinde her bir elemanın aritmetik ortalama ile olan farkının karelerinin toplamının veri adedinin bir eksiğine bölümünün kare köküdür.
Düşük standart sapma değeri, bir araya toplanmış ve ortalamaya daha yakın verilerin çok olduğunun ölçüsüdür. n tane verinin aritmetik ortalaması x olmak üzere, bu veri grubunun standart sapması (s);
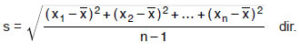
Örnek
1, 7, 8, 9, 10, 13, 50 veri grubunun standart sapmasını bulalım.
Ortalama
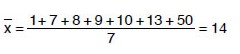
Standart Sapma
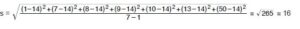
Verilerin Grafikle Gösterilmesi
Histogram Grafiği
Gruplandırılmış bir veri topluluğunda, her bir gruptaki veri sayılarının bitişik dikdörtgen şeklinde sütunlar halinde gösterimidir.
*Histogram genelde sürekli verilerin gösteriminde kullanılır.
*Özellikle veri sayılarının çok olduğu durumlarda tercih edilir.
*Her aralık eşit olarak bölünerek gösterilir.
*Her bir veri için ayrı değil, belirli aralıktaki toplam veri sayısı ile ilgili yorum yapılmasını sağlar.
Histogram oluşturulurken;
1) Öncelikler veriler küçükten büyüğe sıralanır. (İşlemlerde kolaylık sağlar.)
2) Veri grubunun açıklığı (aralığı) bulunur. Açıklık en büyük veriden en küçük verinin çıkartılması ile elde edilir.
3) Verilerin kaç gruba ayrılacağı belirlenir. Veri gruplarının sayısının 10 civarında olması uygundur.
4) Grup genişliği bulunur. Açıklık değerinin grup sayısına bölünmesiyle elde edilen sayıdan büyük en küçük doğal sayı grup genişliği olarak alınır. (Veri gruplarının sayısının 10 alınması hesaplamayı kolaylaştırır.)
5) Veriler en küçük veriden başlayarak grup genişliğine göre gruplara ayrılır.
6) Oluşturulan gruplar ve gruplardaki veri sayıları tablo halinde düzenlenir.
7) Tabloya bakılarak histogram çizilir.
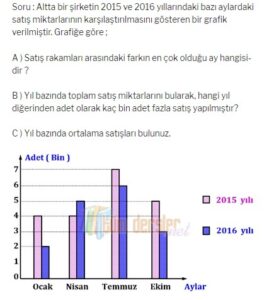
Veri Türleri
Kesikli Veri: Belirli bir aralıktaki her gerçek sayı değerini alamayan veri türüdür. Örneğin bir mağazada satılan ceket sayısı 12,5 olamaz, tam sayı olmak zorundadır. Bir derginin aylık satış sayıları, günlere göre okul kantininden alış-veriş yapan öğrencinin sayıları birer kesikli veridir.
Sürekli Veri: Belirli bir aralıktaki her gerçek sayı değerini alabilen veri türüdür. Bir şehrin aylara göre sıcaklık değişimi, bir bitkinin boyunun yıllara göre değişimi, bir ailenin aylara göre tükettiği elektrik miktarı birer sürekli veridir.
Çizgi Grafiği
Sürekli verilerin yatay ve düşey eksendeki değerleri işaretlenerek bulunan noktaların düz çizgilerle birleştirilmesi sonucunda elde edilen grafik türüdür.

Sütun Grafiği
Veri gruplarını karşılaştırmak için koordinat sisteminde yatay ya da düşey olacak şekilde sütun ya da çubuk kullanılarak çizilen grafik türüdür. Sütun grafiği kesikli veriler için kullanılır.
Daire Grafiği
Verilerin bütüne olan oranını daire dilimleriyle gösteren grafik türüdür. Bütünün parçalarıyla ilgili yorum yapılmasını sağlayan en güçlü yöntemdir.


Hiç yorum yok