Çarpanlara Ayırma

Ortak Parantez Alma

Bir cebirsel ifadenin her bir terimindeki ortak çarpanların, parantez dışına alınıp terimlerin çarpımı biçiminde yazılmasına bu cebirsel ifadeyi ortak çarpan parantezine almak denir.

a.x + b.x – c.x=x(a+b-c)

Örnek:

3x – 6y = 3(x-2y)

4ax – a = a(4x-1)

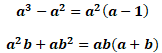
Sadeleştirme

Kesirli ifadelerde pay ve paydada ortak  çarpanlar varsa bu çarpanların birbirlerini yok etmesi işlemine sadeleştirme denir.

Örnek:

işleminin sadeleştirilmiş biçimini bulalım.

Örnek:

işleminin sadeleştirilmiş biçimini bulalım.

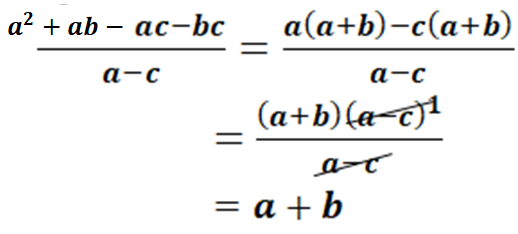
Özdeşlikler

1.İki Kare Farkı

Örnek:

Örnek:

olduğuna göre x.y çarpımının sonucu kaçtır?

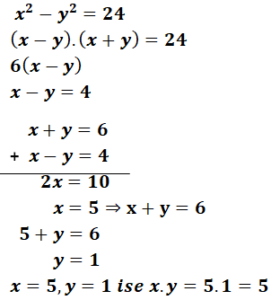
Tam Kare İfadeler

Bu özdeşlikler düzenlenirse;

elde edilir.

Örnek:

a-b=3
a.b=4

olduğuna göre   toplamı kaçtır?

Örnek:

a+b=13
a.b=40

olduğuna göre , a-b farkının pozitif değeri kaçtır?

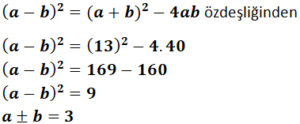
İki Küp Toplamı ve Farkı

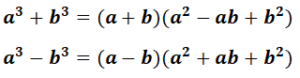
Örnek:

x ve y gerçel sayılar olmak üzere,

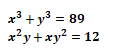
olduğuna göre x+y toplamı kaçtır?

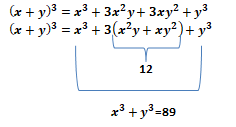
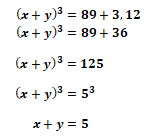
Üç Terimli Bir İfadenin Çarpanlarına Ayrılması

 şeklinde iki durum söz konusudur.

1. Durum

 bu ifadenin çarpanlarına ayrılması

c=m.n
b=m+n olmak üzere

Örnek:

 ifadenin çarpanlarından birini bulalım.

Örnek:

2. Durum

 ifadesinde a≠1 olursa bu ifadenin çarpanlarına ayrılması;

a=k.m
b=k.n+p.m
c=p.n

olmak üzere;
=(k.x+p).(m.x+p) şeklindedir.

Örnek:

 ifadesinin çarpanlardan birini bulalım.

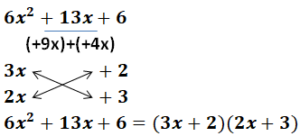
kaynakça:www.basarisiralamalari.com